Drawing Apollonian Gaskets

December 9, 2024

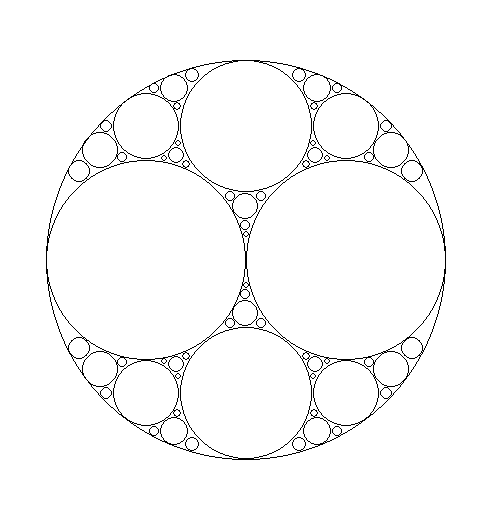
An Apollonian gasket is a fractal formed by recursively adding circles in the gaps between three mutually tangent circles. It creates patterns of ever smaller circles, producing an interesting fractal structure.

The fractal is generated by the following production rules:

1. Start with three circles that are tangent to each other.
2. Calculate the radii and positions of new circles that are tangent to all three.
3. Form new sets of 3 circles using the existing circles and the new circles.
4. Recursively repeat the process.

We’ll implement these rules in python.

First, let’s define what a circle is. A circle is defined by its center point and its curvature. The curvature of a circle is the reciprocal of its radius: positive for the outside of the circle and negative for the inside of the circle. Two circles are considered tangent if they touch at exactly one point. We’ll use complex numbers to represent the center of each circle, where the real part represents the x-coordinate and the imaginary part represents the y-coordinate. This simplifies the mathematical equations we’ll soon see.

import math, cmath

class Circle:
    def __init__(self, x, y, curvature):
        self.center = complex(x, y)
        self.curvature = curvature
        self.radius = abs(1 / curvature) # Obviously can't have a negative radius

Now let’s define an initial set of 3 circles. These circles can be any size or position as long as they’re all mutually tangent.

# Example circles
c1 = Circle(300, 300, -1/200)  # Outer circle
c2 = Circle(200, 300,  1/100)  # Left inner circle
c3 = Circle(400, 300,  1/100)  # Right inner circle
circles = [c1, c2, c3]

Before we get into the math, let’s visualize the circles using pygame:

import pygame

pygame.init()
window = pygame.display.set_mode((600, 600))

running = True
while running:
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            running = False

    window.fill((255, 255, 255))

    for circle in circles:
        x, y = circle.center.real, circle.center.imag
        pygame.draw.circle(window, (0, 0, 0), (x, y), circle.radius, 1)

    pygame.display.update()

At this point, you should see the initial three circles on the screen.

Next, we want to compute the curvature and position of the next circle. To compute the curvature of a new circle that fits into the gap, we can use Descartes’ Theorem. It states:

\[(k_1 + k_2 + k_3 + k_4)^2 = 2(k_1^2 + k_2^2 + k_3^2 + k_4^2)\]

where \(k_1, k_2, k_3, k_4\) are circle curavtures.

Solving for \(k_4​\), we get:

\[k_4 = k_1 + k_2 + k_3 \pm 2 \sqrt{k_1 k_2 + k_2 k_3 + k_1 k_3}\]

Implemented here:

def descartes_theorem(k1, k2, k3):
    x = k1 + k2 + k3
    discriminant = abs(k1 * k2 + k2 * k3 + k3 * k1)
    y = 2 * math.sqrt(discriminant)
    return [x + y, x - y]

This quadratic equation provides two possible curvatures, corresponding to the two circles that can fit in the gap.

Now that we have the circle’s curvature, we can find its position. To find the position of the new circle, we can extend Descartes’ theorem to the complex plane:

\[(k_1 z_1 + k_2 z_2 + k_3 z_3 + k_4 z_4)^2 = 2(k_1^2 + k_2^2 + k_3^2 + k_4^2)\]

where \(k_1, k_2, k_3, k_4\) are curvatures and \(z_1, z_2, z_3, z_4\) are positions. Notice that positions are complex numbers.

Solving for \(z_4\), we get:

\[z_4 = \frac{z_1 k_1 + z_2 k_2 + z_3 k_3 \pm 2 \sqrt{k_1 k_2 z_1 z_2 + k_2 k_3 z_2 z_3 + k_1 k_3 z_1 z_3}}{k_4}\]

Implemented here:

def complex_descartes_theorem(z1, k1, z2, k2, z3, k3, k4):
    zk1 = z1 * k1
    zk2 = z2 * k2
    zk3 = z3 * k3

    x = zk1 + zk2 + zk3
    y = 2 * cmath.sqrt(zk1 * zk2 + zk2 * zk3 + zk3 * zk1)

    return [(x + y) / k4, (x - y) / k4]

Now we can define a function to get all the 4 possible circles from 3 mutually tangent circles. There’s 4 possible circles because there’s 2 curvatures and 2 center points to choose from.

def find_next_circles(c1, c2, c3):
    k1, k2, k3 = c1.curvature, c2.curvature, c3.curvature
    z1, z2, z3 = c1.center, c2.center, c3.center

    curvatures = descartes_theorem(k1, k2, k3)
    circles = []

    for k in curvatures:
        z4, z5 = complex_descartes_theorem(z1, k1, z2, k2, z3, k3, k)
        circles.append(Circle(z4.real, z4.imag, k))
        circles.append(Circle(z5.real, z5.imag, k))

    return circles

To ensure that the new circle positions are valid, we’ll need to check if they’re tangent to the existing circles. We’ll define a helper function for this:

def tangential(c1, c2):
    epsilon = 0.1
    r1 = c1.radius
    r2 = c2.radius
    distance = abs(c1.center - c2.center) # euclidean distance
    case1 = abs(distance - (r1 + r2)) < epsilon # c1 and c2 are adjacent
    case2 = abs(distance - abs(r2 - r1)) < epsilon # c2 is inside c1
    return case1 or case2

For optimization reasons we’ll also want to check if we’ve already generated a similar circle:

def alreadyExists(circles, circle):
    epsilon = 0.1
    for other in circles:
        distance = abs(circle.center - other.center)
        if distance < epsilon:
            return True
    return False

Finally, we can recursively generate the Apollonian gasket:

def generate_gasket(circles, c1, c2, c3, depth):
    if depth <= 0:
        return

    next_circles = find_next_circles(c1, c2, c3)

    for c in next_circles:
        too_small = c.radius < 3
        mutually_tangential = all(tangential(c, x) for x in [c1, c2, c3])
        if not mutually_tangential or too_small or alreadyExists(circles, c):
            continue

        circles.append(c)

        # Generate with new sets of 3 circles
        generate_gasket(circles, c1, c2, c, depth - 1)
        generate_gasket(circles, c2, c3, c, depth - 1)
        generate_gasket(circles, c1, c3, c, depth - 1)

generate_gasket(circles, c1, c2, c3, 4)

Run the program, and you should see this fractal:

The full source code can be found here.